1. Основные соотношения
Пусть источники распределены по небу равномерно, а их статистика в зависимости от плотности потока S определяется функцией n(S), представляющей собой среднее количество источников на единицу потока в одном стерадиане.
Найдём стандартное отклонение сигнала дискретных источников
на выходе радиотелескопа с диаграммой направленности ![]() .
.
Рассмотрим следующую упрощённую ситуацию. Пусть диапазон
потоков ограничен промежутком ![]()
![]() ,
и источники распределены равномерно в конечной области
,
и источники распределены равномерно в конечной области ![]() ,
размер которой существенно превышает размер диаграммы направленности. Предположим
также, что в области W. находится
ровно N источников, причём
,
размер которой существенно превышает размер диаграммы направленности. Предположим
также, что в области W. находится
ровно N источников, причём
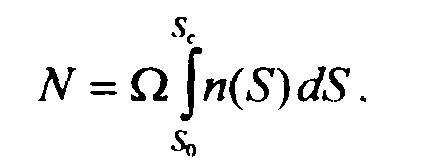

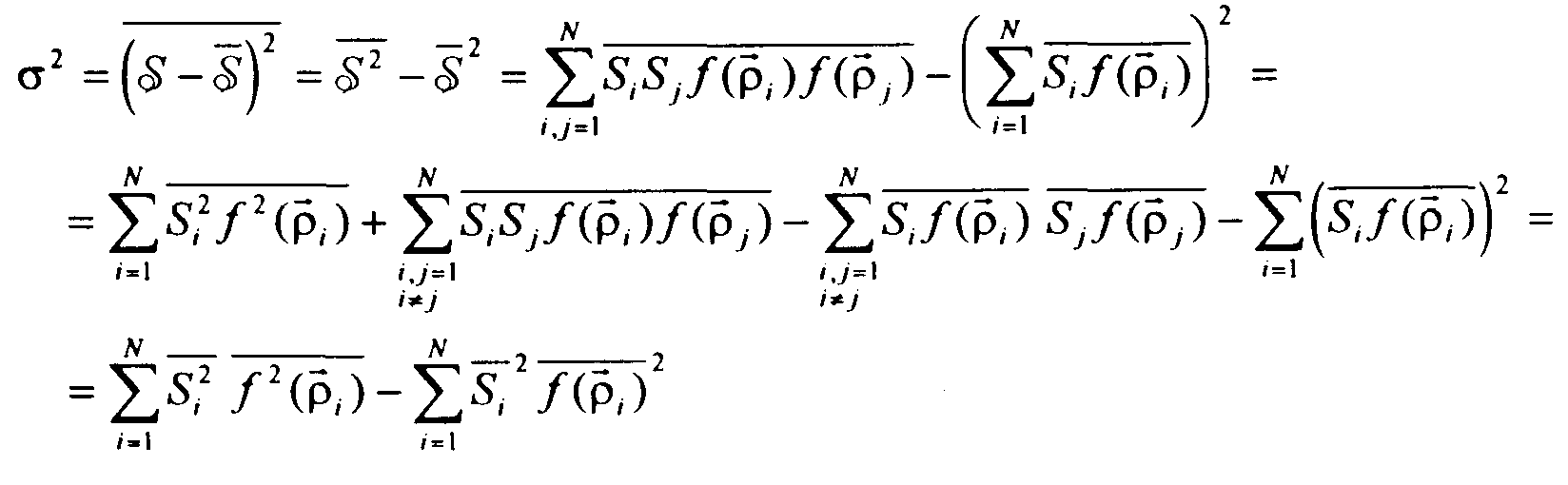
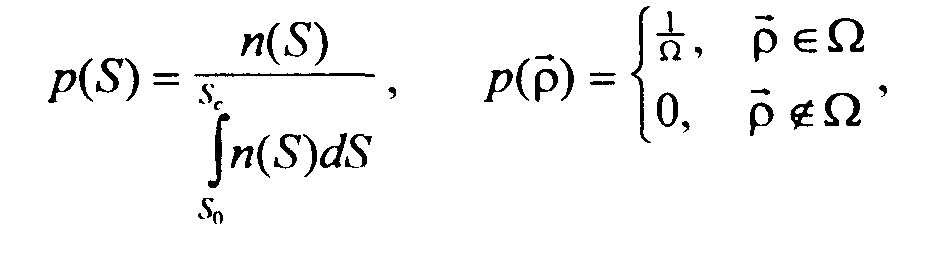
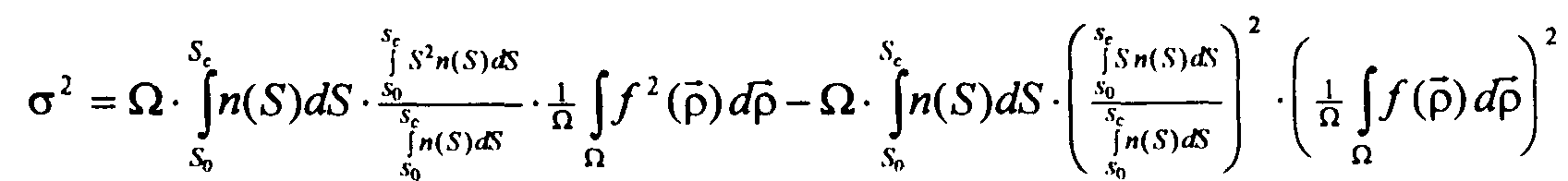
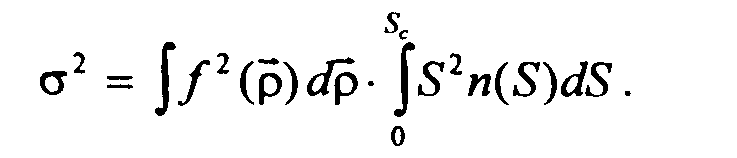

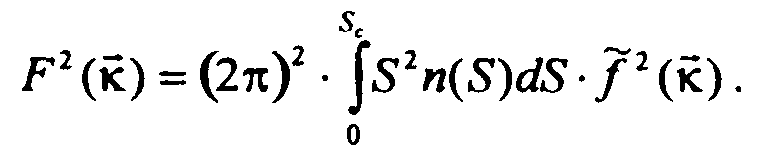
Выражения (1.1) и (1.3) даны в единицах потока; для перехода
втемпературные единицы необходимо умножить на [Aeff/2k)2
, где Аeff—эффективная площадь апертуры, k —
постоянная Больцмана.
2. Методы оценки амплитуды сигнала дискретных источников
Интегральные свойства зависимости LogN/LogS таковы, что основной вклад в амплитуду сигнала вносят самые яркие источники, оставшиеся в записи, и, следовательно, включать в расчёты сразу всю эту кривую нельзя (кроме того, при больших потоках LogN/LogS вообще теряет физический смысл). Поэтому в само определение такой оценки приходится включать способ, которым обрезается "яркий хвост" LogN/LogS (это, как правило, способ определения граничного потока S0 в выражении для дисперсии сигнала (1.1)). Таких способов можно предложить несколько и выбор какого-либо из них зависит от специфики конкретного приложения.
Перечисленные ниже методы (кроме первого) так или иначе
решают вопрос о выборе граничного потока, поэтому, в соответствии с (1.3),
каждому такому способу отвечает своя амплитуда спектра сигнала от дискретных
источников. Таким образом, эти методы можно использовать также для определения
предела
спектральной чувствительности инструмента, обусловленного шумом
дискретных источников.
2.1. Оценка сигнала при заданном уровне чистки (селекция по отклику)
Оценка, предложенная в работе [1], основана на предположении, что источники с откликом в данной точке, превышающим некоторую величину, удаляются. Можно предположить, что чистка проводится до тех пор, пока отношение максимального отклика к среднеквадратичному не становится равным заранее заданной величине т, называемой уровнем чистки. При этом среднеквадратичный сигнал ? можно вычислить как функцию уровня чистки, диаграммы направленности и LogN/LogS, если численно решить следующее уравнение:
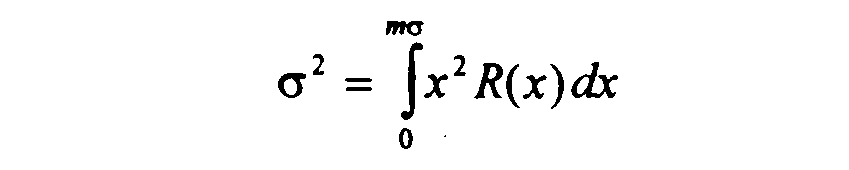
2.2. Оценка сигнала при заданном уровне
чистки (селекция по потоку)
![]()
Отметим, что для определения предела чувствительности радиотелескопа, связанного с дискретными источниками, больше остальных подходит именно эта оценка при небольших значениях уровня чистки (m = 2 -3 ).
Определённый интерес представляет вариант оценки, связанный с предварительной селекцией площадки наблюдения. Рассмотрим площадку конечных размеров W.
Среднее количество источников с потоком, превышающим Sc,
в площадке W,
равно
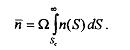
Выпишем вероятность того, что их окажется ровно п
(распределение Пуассона):
![]()
Приравнивая п к нулю, получим вероятность Pc
того, что в площадке W
не окажется источников с потоком, превышающим Sc:

Отсюда можно найти (по крайней мере численно) и обратную зависимость, то есть граничный поток как функцию частоты, с которой встречается соответствующая ему площадка.
Зная Sc , с помощью (1.1) можно вычислить среднеквадратичный сигнал;
таким образом, последний оказывается связанным с "вероятностью площадки".
2.4. Оценка сигнала при заданном граничном потоке
Самый очевидный вариант оценки получается, если напрямую задавать граничный поток S^ и вычислять среднеквадратичный сигнал в соответствии с

3. Зависимость LogN/LogS
В данной работе используется модель LogN/LogS Франческини и др. [1]. В рамках этой модели рассматривается 5 популяций дискретных источников: квазары и эллиптические галактики с крутым спектром, квазары и эллиптические галактики с плоским спектром, галактики с активным звездообразованием, сейфертовские галактики, спиральные галактики.
С точки зрения радиочастотного спектрального индекса a эти объекты можно разделить на две популяции: источники с крутым спектром (a~ 0.9) и источники с плоским спектром (a~ О). Соответствующие этим популяциям зависимости n(S) приведены на Рис. 1.
Отдельные компоненты LogN/LogS пересчитываются на другую длину волны следующим образом:
4. Интегральный предел чувствительности
РАТАНа-600
Основным режимом РАТАНа-600, в котором проводятся эксперименты, связанные с достижением предельной чувствительности, следует считать режим наблюдения с одиночным сектором.
Здесь рассматриваются оценки сигнала фоновых источников, рассчитанные для этого случая с помощью аппроксимации диаграммы направленности и LogN/LogS из раздела 3.
В Табл. 1 приведены значения среднеквадратичного сигнала дискретных источников s
для трех различных уровней чистки (т= 2,3,5, см. раздел 2.2) и трёх
вероятностей (частот) площадки длиной 15° и шириной, равной вертикальному охвату диаграммы направленности HPBWE (PW=0.25,05,0.75, см. раздел 2.3). Длина
площадки приблизительно соответствует длине стандартного скана длиной в 1 час на небольшом склонении.
Табл. 1. Среднеквадратичная амплитуда сигнала фоновых
радиоисточников s для различных частотных
каналов РАТАНа-600 в режиме одиночного сектора (высота 50").
| s mJy | Sc, mJy | ||||||||||
| a, cm | m | PW (?=HPBWE-15°) | PW (?=HPBWE-15°) | K/Jy | K/Jy | ||||||
| 2 | 3 | 5 | 0.25 | 0.5 | 0.75 | 0.25 | 0.5 | 0.75 | Еа=1 | ||
| 0.8 | З.бОе-5 | 9.93е-5 | 3.54е-4 | 0.139 | 0.187 | 0.262 | 43.5 | 80.0 | 163. | 0.068 | 0370 |
| 1.0 | 8.88е-5 | 2.53е^” | 8.68е-4 | 0.202 | 0.266 | 0.365 | 54.8 | 986 | 195. | 0.085 | 0.372 |
| 1.38 | 3.78е-4 | 1.00е-3 | 289е-3 | 0.349 | 0.448 | 0595 | 77.5 | 135. | 258. | 0 118 | 0367 |
| 2.08 | 2.14е-3 | 4.71е-3 | 1.07е-2 | 0.717 | 0.889 | 1.129 | 123. | 205. | 373. | 0.171 | 0.348 |
| 2.7 | 5.04е-3 | 1.01е-2 | 2.06е-2 | 0.988 | 1.21 | 1.52 | 131. | 215. | 387. | 0.272 | 0460 |
| 3.9 | 1.59е-2 | 2.81е-2 | 522е-2 | 1.74 | 208 | 2.55 | 170. | 271. | 473. | 0.379 | 0563 |
| 6.0 | 607е-2 | 9.78е-2 | 0.172 | 4.02 | 4.68 | 5.49 | 305. | 467. | 768. | 0344 | 0.481 |
| 7.6 | 0.124 | 0.195 | 0.337 | 658 | 7.53 | 868 | 445. | 669. | 1070. | 0297 | 0408 |
| 8.2 | 0.152 | 0.236 | 0.409 | 7.47 | 8.52 | 980 | 476. | 714. | 1140. | 0.310 | 0.424 |
| 11.0 | 0.349 | 0.538 | 0.977 | 13.3 | 15.0 | 17.0 | 716. | 1060. | 1660. | 0.283 | 0387 |
| 13.0 | 0.560 | 0.859 | 1.65 | 18.5 | 20.7 | 23.3 | 905. | 1330. | 2050. | 0.269 | 0.369 |
| 18.0 | 1.35 | 2.15 | 4.82 | 33.7 | 37.4 | 41.7 | 1320. | 1920. | 2930. | 0.276 | 0396 |
| 21 0 | 2.00 | 3.33 | 8.03 | 43.8 | 486 | 54 1 | 1510 | 2190 | 3350. | 0301 | 0447 |
| 31.0 | 5.43 | 10.2 | 25.2 | 81.5 | 90.4 | 101. | 1970. | 2870. | 4430. | 0.479 | 0.716 |
Первый вариант оценки соответствует глубокой двумерной обработке записей алгоритмом типа CLEAN и значение m показывает, во сколько раз наименьшая амплитуда удалённых источников превышает среднеквадратичный сигнал. Значение m = 2 соответствует физическому пределу чувствительности инструмента. Второй вариант соответствует селекции сканов длиной 15° по среднеквадратичному вкладу дискретных источников, причём в среднем доля сканов со среднеквадратичным сигналом не более указанного в таблице значения составляет РW..
В таблице также приведены значения граничного потока, соответствующие РW, и коэффициенты пересчёта из единиц потока в температурные единицы для реальной и идеальной (ea= 1) эффективности апертуры.
Интересен также и рекордный режим "Зенит", при котором наблюдения осуществляются с помощью полного кольца. В этом случае предел чувствительности (при m=2) составляет 1.45-10– 8 Jy на длине волны 8.2 см, что при эффективной площади 10000 кв.м. соответствует 5.25-10–8К.
5. Предел чувствительности РАТАНа-600 по угловому спектру
Найденные в предыдущем разделе значения сигнала фоновых источников относятся к так называемой "полной флуктуации", то есть к интегралу углового спектра мощности. Эти значения важны в том случае, когда используется весь диапазон масштабов, доступный данному инструменту. Однако во многих задачах это не так:
например, при исследовании сахаровских осцилляций (с характерным масштабом более 0°2) на РАТАНе-600 имеет место избыточное разрешение. В этом случае следует учитывать локальное поведение спектра мощности шума дискретных источников, форма которого задаётся диаграммой направленности инструмента, а амплитуда — граничным потоком (см. (1.3)).
В случае пассажного инструмента, каким является РАТАН-600,
наибольший интерес представляет одномерный угловой спектр, взятый в горизонтальном
направлении. С учётом (1.3), (А.З), (В. 15), для такого спектра имеем следующее
выражение:
В Табл. 2 приведены значения амплитуды спектра сигнала
дискретных источников для тех же режимов работы с этим сигналом, что и
в предыдущем разделе. Как и ранее, значение при т = 2 характеризует
физический предел чувствительности.
Табл. 2. Значения амплитуды одномерного углового спектра
сигнала фоновых источников для различных частотных каналов РАТАНа-600 в
режиме одиночного сектора (высота 50°)
| F0,mk | ||||||
| l, cm | m | PW (W=HPBWE-15°) | ||||
| 2 | 3 | 5 | 0.25 | 0.5 | 0.75 | |
| 0.8 | 7.49е-5 | 2.076-4 | 7.376-4 | 0.289 | 0.389 | 0.545 |
| 1.0 | 2.07е-4 | 5.906-4 | 2.026-3 | 0.471 | 0.620 | 0.851 |
| 1.38 | 1.03e-3 | 2.716-3 | 7.85е-3 | 0.948 | 1.22 | 1.61 |
| 2.08 | 6.906-3 | 1 526-2 | 3.45е-2 | 2.31 | 2.86 | 3.64 |
| 2.7 | 2.21е-2 | 443е-2 | 9.046-2 | 433 | 5.31 | 6.67 |
| 3.9 | 9556-2 | 0.169 | 0.313 | 10.4 | 12.5 | 15.3 |
| 6.0 | 0.408 | 0.658 | 1.16 | 27.1 | 31.4 | 36.9 |
| 76 | 0845 | 1.33 | 2.30 | 44.9 | 51.3 | 59.1 |
| 8.2 | 1.10 | 1.71 | 2.97 | 542 | 61.8 | 71.1 |
| 11.0 | 2.77 | 4.27 | 7.75 | 105. | 119. | 135. |
| 13.0 | 4.68 | 7.19 | 13.8 | 155. | 173. | 196. |
| 18.0 | 13.9 | 22.1 | 49,6 | 347. | 385. | 429. |
| 21.0 | 24.0 | 40.0 | 96.5 | 527. | 584. | 650. |
| 31.0 | 107. | 202. | 499. | 1610. | 1790. | 2000. |
Отметим, что на масштабах сахаровских осцилляций для сантиметровых каналов переменный множитель в (5.1) приближённо равен единице и спектр представляет собой горизонтальную прямую на уровне F02 .
Литература
1. Коваленко И.Н., Кузнецов Н.Ю., Шуренков В.М., Случайные процессы. Справочник. Наукова думка, 1983.
2. Bersanelli M. et al, COBRAS/SAMBA, A Mission Dedicated to Imaging the Anisotropies of the Microwave Background, Preprint ESA D/SCI(96)3, 1996.
3ю Franceschini A. Et al, The Astrophysical Journal, 344, 35, 1989.
Приложение 2. Компьютерное моделирование многочастотного
обзора на радиотелескопе РАТАН-600
Разложим реализацию некоторого стационарного случайного процесса
Ь(![]() )
в ряд Фурье на прямоугольнике размерами (X,Y). На спектральной плоскости
этому разложению будет соответствовать функция
)
в ряд Фурье на прямоугольнике размерами (X,Y). На спектральной плоскости
этому разложению будет соответствовать функция ![]() ,
определенная на узлах
,
определенная на узлах ![]() периодической
двумерной решетки с элементарной ячейкой размерами (2?/?,
2?/Y).
периодической
двумерной решетки с элементарной ячейкой размерами (2?/?,
2?/Y).
![]()
Для выяснения природы коэффициентов ![]() ,
рассмотрим интегральную сумму спектрального представления :
,
рассмотрим интегральную сумму спектрального представления :
![]()
Величины ![]() обладают следующим свойством :
обладают следующим свойством :
![]()
где ![]() —спектр
мощности процесса
—спектр
мощности процесса ![]() .
.
Кроме того, если ![]() —
гауссовский процесс, то
—
гауссовский процесс, то ![]() —
нормально распределённые комплексные величины (см. [1]).
—
нормально распределённые комплексные величины (см. [1]).
Будем считать, что разбиение спектральной плоскости в интегральной сумме (1.2) такое же, как и в разложении (1.1). В этом случае получим:
![]() (1.4)
(1.4)
При этом в соответствии с (1.3) должно выполняться
![]() (1.5)
(1.5)
Таким образом, для стационарного гауссовского процесса ![]() коэффициенты
коэффициенты ![]() представляют
собой независимые нормально распределённые случайные величины со средним
квадратом модуля, определяемым выражением (4.1.5).
представляют
собой независимые нормально распределённые случайные величины со средним
квадратом модуля, определяемым выражением (4.1.5).
При моделировании величин ![]() их действительная и мнимая части генерируются по отдельности как независимые
нормально распределённые величины с
их действительная и мнимая части генерируются по отдельности как независимые
нормально распределённые величины с
1
дисперсией ![]() и
нулевым средним. При этом для действительного процесса следует
и
нулевым средним. При этом для действительного процесса следует
учесть, что ![]() .
Для ограничения количества членов в сумме (1.1) нужно задаться каким-либо
минимальным характерным размером L.. В этом случае надо учитывать
только те точки
.
Для ограничения количества членов в сумме (1.1) нужно задаться каким-либо
минимальным характерным размером L.. В этом случае надо учитывать
только те точки ![]() , которые
находятся внутри квадрата со стороной 2?/
L и центром в начале координат.
, которые
находятся внутри квадрата со стороной 2?/
L и центром в начале координат.
При вычислении сигнала ![]() на выходе инструмента с диаграммой направленности
на выходе инструмента с диаграммой направленности ![]() следует
пользоваться следующим соотношением:
следует
пользоваться следующим соотношением:
![]()
где ![]() —
преобразование Фурье диаграммы направленности.
—
преобразование Фурье диаграммы направленности.
Пусть нам известны нормированная на значение в нуле диаграмма
направленности инструмента ![]() (0 ?
(0 ? ![]() ? 1;
?(
? 1;
?(![]() = 1;
= 1; ![]() — двумерный радиус-вектор на "плоском" небе) и дифференциальная зависимость
количества радиоисточников на единичной площади от плотности потока n(S)
. Располагая этими данными, мы хотим научиться моделировать сигнал
на выходе радиотелескопа таким образом, чтобы он в некотором смысле был
"как настоящий". Лучше всего было бы заполнить всё небо радиоисточниками
в соответствии с их статистикой и свернуть эту картину с диаграммой направленности.
Но это невозможно, во-первых, потому что небо слишком велико, и, во-вторых,
потому что слишком велика плотность слабых источников. Следовательно, если
мы хотим справиться с вычислениями, источники нужно учитывать только в
некоторой окрестности ? точки
наблюдения и только начиная с некоторого минимального потока S0
. Слова "как настоящий" в этом случае означают, что средний квадрат
отклика от неучтенных источников не должен превышать заданной величины.
Кроме того, разумно ограничить область потоков сверху: мы как бы считаем,
что область наблюдения выбрана так, что в ней источники ярче Sc
отсутствуют (мы также не будем учитывать вклад таких источников в ошибку
моделирования).
— двумерный радиус-вектор на "плоском" небе) и дифференциальная зависимость
количества радиоисточников на единичной площади от плотности потока n(S)
. Располагая этими данными, мы хотим научиться моделировать сигнал
на выходе радиотелескопа таким образом, чтобы он в некотором смысле был
"как настоящий". Лучше всего было бы заполнить всё небо радиоисточниками
в соответствии с их статистикой и свернуть эту картину с диаграммой направленности.
Но это невозможно, во-первых, потому что небо слишком велико, и, во-вторых,
потому что слишком велика плотность слабых источников. Следовательно, если
мы хотим справиться с вычислениями, источники нужно учитывать только в
некоторой окрестности ? точки
наблюдения и только начиная с некоторого минимального потока S0
. Слова "как настоящий" в этом случае означают, что средний квадрат
отклика от неучтенных источников не должен превышать заданной величины.
Кроме того, разумно ограничить область потоков сверху: мы как бы считаем,
что область наблюдения выбрана так, что в ней источники ярче Sc
отсутствуют (мы также не будем учитывать вклад таких источников в ошибку
моделирования).
Обычно поступают так: окружают точку наблюдения прямоугольной
областью, в которой воспроизводят заданную статистику радиоисточников в
диапазоне от. S0 до Sc .
Вначале генерируется количество источников N,
оно распределено по закону Пуассона со средним значением, равным
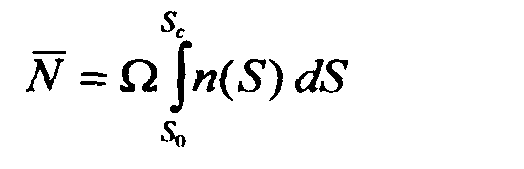
имеет плотность распределения ?,?n(S)
/ ![]() в промежутке [S0, Sc]. Затем, используя ?(
в промежутке [S0, Sc]. Затем, используя ?(![]() ,
вычисляют сумму откликов от всех источников. Далее точку наблюдения вместе
,
вычисляют сумму откликов от всех источников. Далее точку наблюдения вместе
с областью ? сдвигают в новое место, и все повторяется сначала (если
новая область ?'
пересекается с прежней, то источники, принадлежащие
?'![]() ?, сохраняются, и новые
источники генерируются только в ?' \ (?'
?, сохраняются, и новые
источники генерируются только в ?' \ (?' ![]() ?)).
?)).
В этом подходе область генерирования источников одинакова
для всех S ![]() [S0 ,Sc].
Это удобно для программирования, но содержит неоправданную избыточность:
очевидно, что слабые источники можно учитывать в меньшем "окне", чем сильные.
При высоких требованиях к точности моделирования такая избыточность может
привести (и приводит) к неприемлемому времени счета.
[S0 ,Sc].
Это удобно для программирования, но содержит неоправданную избыточность:
очевидно, что слабые источники можно учитывать в меньшем "окне", чем сильные.
При высоких требованиях к точности моделирования такая избыточность может
привести (и приводит) к неприемлемому времени счета.
Для более эффективного алгоритма следует считать область ? зависящей от S , что в рудиментарном виде присутствует и в традиционном способе моделирования, ведь в этом случае
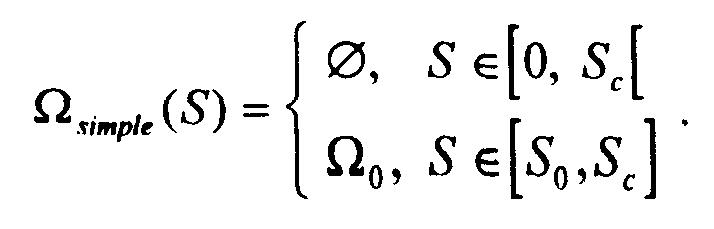
Отсюда видно, что задачи определения области генерирования и определения начального потока — это одна и та же проблема отыскания оптимальной в некотором смысле функции ?(S) на промежутке [О, Sc ]. Рассмотрим эту задачу подробнее.
Определим условия, которым должна удовлетворять ?(S). Одно условие известно: ошибка моделирования (т.е. средний квадрат вклада неучтенных источников) должна равняться фиксированной величине. Очевидно, что одного этого недостаточно для определения ?(S). Например, для любой заданной ошибки моделирования можно найти соответствующие ей параметры S0 и ?0 выражении для ?simple; существуют и другие, еще менее эффективные варианты.
3
Поскольку нас интересует вычислительная эффективность
алгоритма, в качестве второго условия потребуем минимизации соответствующего ![]() (S)
среднего количества источников.
(S)
среднего количества источников.
Таким образом, мы сформулировали следующую вариационную задачу:
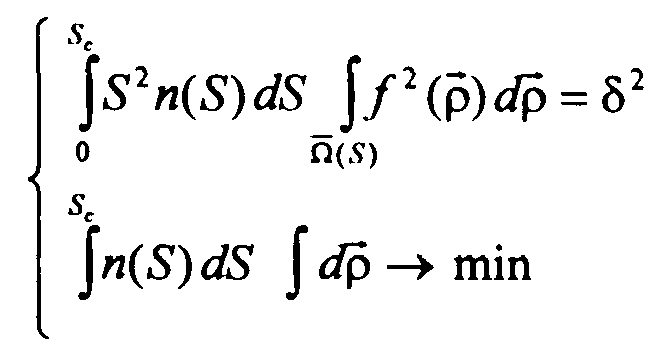
(![]() — точность
моделирования).
— точность
моделирования).
Искомый объект ![]() — это некая область в трехмерном пространствене
— это некая область в трехмерном пространствене ![]() ,
не обязательно связная. Попробуем выяснить что-нибудь о сечении этой области
какой-либо плоскостью, перпендикулярной оси S. Для этого предположим,
что нам известно значение F внутреннего интеграла в (2.1а) при каком-либо
фиксированном значении S, и при этом условии будем минимизировать
вклад площади соответствующего сечения
,
не обязательно связная. Попробуем выяснить что-нибудь о сечении этой области
какой-либо плоскостью, перпендикулярной оси S. Для этого предположим,
что нам известно значение F внутреннего интеграла в (2.1а) при каком-либо
фиксированном значении S, и при этом условии будем минимизировать
вклад площади соответствующего сечения ![]() в выражение (2.1Ь). Другими словами, будем искать область
в выражение (2.1Ь). Другими словами, будем искать область![]() ,
удовлетворяющую условиям
,
удовлетворяющую условиям
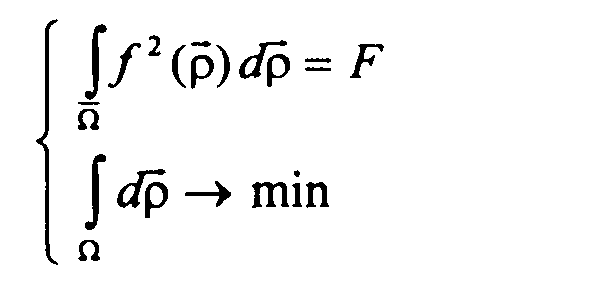
Докажем, что искомая область ограничена изолинией диаграммы направленности
некоторого уровня ![]()
![]() ,
т.е.
,
т.е.
![]()
Пусть найдена константа ![]() ,
при которой область вида (2.3) удовлетворяет соотношению (2.2а) (это можно
сделать: при изменении
,
при которой область вида (2.3) удовлетворяет соотношению (2.2а) (это можно
сделать: при изменении ![]() от 0 до 1 левая часть (2.2а) монотонно уменьшается от максимального значения,
соответствующего интегралу по всей плоскости, до нуля, оставаясь непрерывной).
Докажем, что при этом также выполняется и (2.2Ь). Деформируем область
от 0 до 1 левая часть (2.2а) монотонно уменьшается от максимального значения,
соответствующего интегралу по всей плоскости, до нуля, оставаясь непрерывной).
Докажем, что при этом также выполняется и (2.2Ь). Деформируем область ![]() так, чтобы (2.2а) не нарушалось (см. Рис. 1). Тогда интеграл
так, чтобы (2.2а) не нарушалось (см. Рис. 1). Тогда интеграл ![]() от
по участкам вида 1
от
по участкам вида 1 ![]() должен
совпадать с интегралом по участкам вида 2. Но так как любое значение
должен
совпадать с интегралом по участкам вида 2. Но так как любое значение ![]() вне
вне ![]() меньше, чем внутри,
то суммарная площадь участков 2 будет больше площади участков 1.
меньше, чем внутри,
то суммарная площадь участков 2 будет больше площади участков 1.
4
Таким образом, при любой деформации области вида (2.3) при сохранении условия (2.2а) ее площадь растет, то есть (2.2b) для такой области также выполняется.
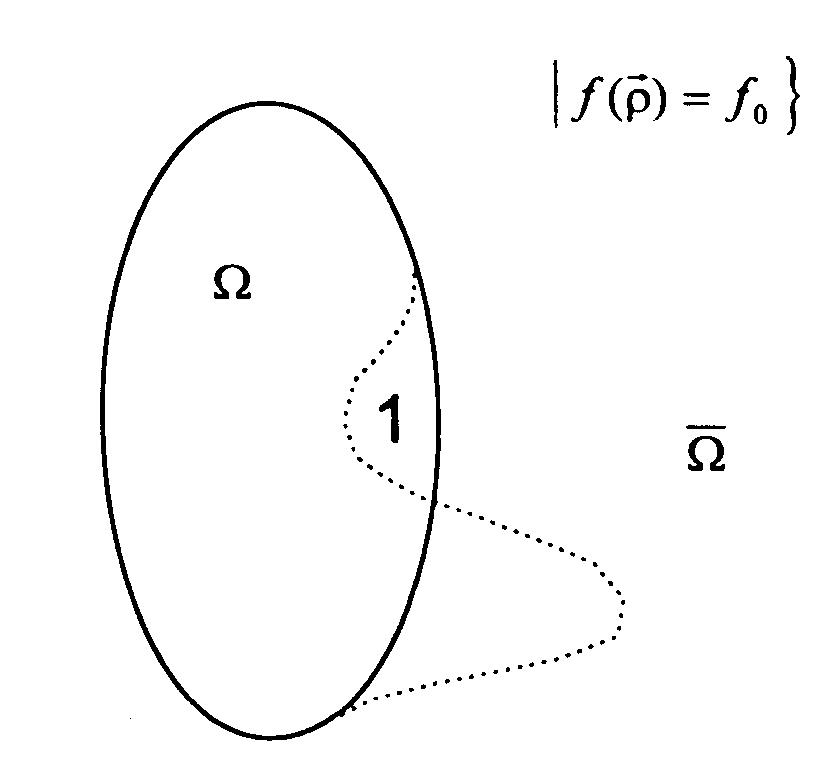
![]()
Рис. 1. К определению оптимальной области генерирования источников
Перепишем (2.1) с учетом (2.3):
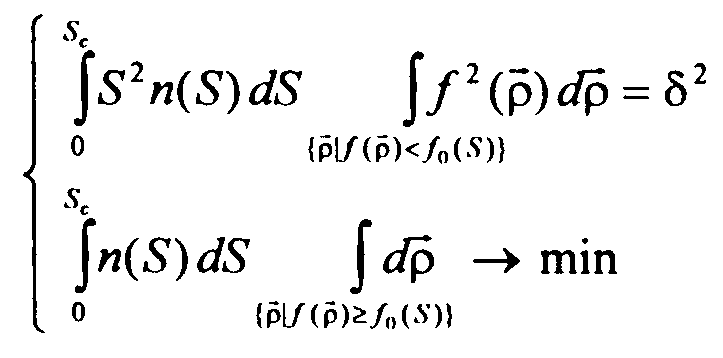
Задача упростилась: остается найти зависимость параметра f0 от S .
В системе (2.4) области интегрирования и подынтегральные
выражения зависят от ![]() только
через функцию f(
только
через функцию f(![]() ), поэтому
следует перейти к интегрированию по значениям f. Это возможно, если
учесть что
), поэтому
следует перейти к интегрированию по значениям f. Это возможно, если
учесть что
![]()
где
![]()
Выражение (2.6) можно получить непосредственно, сопоставляя
с элементом df соответствующий объект ![]() ,
либо традиционным способом, рассматривая преобразование координат
,
либо традиционным способом, рассматривая преобразование координат ![]() = [х,у) —> {x,f(x,y)).
= [х,у) —> {x,f(x,y)).
Отметим наиболее важные свойства функции q(f).
Исходная функция ![]() имеет
множество значений 0,1 и интегрируема на всей плоскости. Для нас также
имеет
множество значений 0,1 и интегрируема на всей плоскости. Для нас также
достаточно, что она непрерывна на плоскости вместе со
всеми своими производными (на самом деле выполняется более сильное условие:
диаграмма направленности должна иметь финитный спектр). При этих условиях
q(f)
определена на открытом промежутке ]0, l[, за исключением не более чем счетного
множества разрывов I рода и интегрируемых разрывов II рода (точечные экстремумы
и седловые точки ?(![]() соответствуют
разрывам I рода, а протяженные экстремумы — разрывам II рода). Интеграл
от q(?) расходится в точке
? = 0; функция ? • q(f)
интегрируема на [0, 1].
соответствуют
разрывам I рода, а протяженные экстремумы — разрывам II рода). Интеграл
от q(?) расходится в точке
? = 0; функция ? • q(f)
интегрируема на [0, 1].
В отдельных случаях q(f) можно вычислить аналитически. Например, для f(x,y) = exp(-a2x2- b2y2) эта функция имеет вид q(f) == ?/(ab • ?).
Итак, с учетом (2.5), выражения (2.4) примут вид

Отметим, что формулировка данной задачи такая же, как и у задачи (2.2):
некое множество нужно разделить на две взаимодополняющие области, минимизируя площадь одной из них при фиксированном значении интеграла от некоторой положительной функции по другой области (n(S) и q(?) в данном случае задают меру на множестве {(S,f|\0<S<Sc & 0 <?<!}). Ответ уже известен — такие области разделяются некоторой изолинией подынтегральной функции, т.е. в случае системы (2.7) — кривой S2?2 = const.
Таким образом, мы получили:
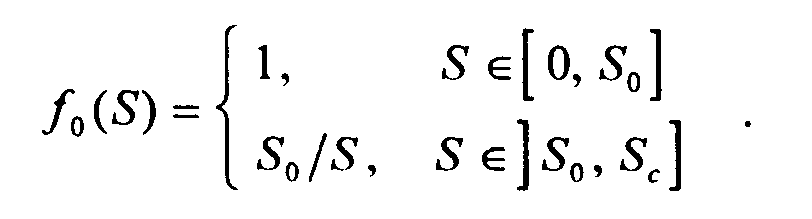
Теперь мы можем сформулировать следующее утверждение. Для получения оптимальной в смысле минимизации среднего количества учитываемых источников модели сигнала, в качестве окна генерирования источников потока S следует брать область, ограниченную изолинией диаграммы направленности уровня fo(S) ( см. (2.8)). При этом средний квадрат вклада
неучтенных источников дается выражением
6
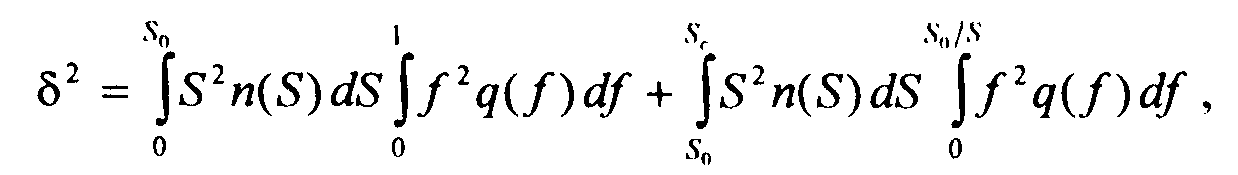
где q{f) находится из диаграммы направленности с помощью (2.6).
Обратив выражение (2.9) численно относительно параметра S0 , мы можем получить его
значение при заданной ошибке моделирования ?2. Далее мы можем использовать описанную ранее процедуру генерирования сигнала с тем уточнением. что площадь и форма окна теперь зависят от S известным образом.
Отметим, что в реальном алгоритме в качестве ?(![]() можно использовать приближенную функцию, мажорирующую реальную диаграмму
направленности. Хотя при этом увеличится количество "обслуживаемых" источников,
можно получить экономию времени за счет более простого вида области генерирования
?(S)
(длясвертки с источниками, конечно, нужно использовать реальную диаграмму
направленности). Соотношение (2.9) при этом работает как верхняя оценка
ошибки моделирования.
можно использовать приближенную функцию, мажорирующую реальную диаграмму
направленности. Хотя при этом увеличится количество "обслуживаемых" источников,
можно получить экономию времени за счет более простого вида области генерирования
?(S)
(длясвертки с источниками, конечно, нужно использовать реальную диаграмму
направленности). Соотношение (2.9) при этом работает как верхняя оценка
ошибки моделирования.
Аналогичный подход используется в том случае, когда у
инструмента есть несколько каналов наблюдения, каждый из которых имеет
свою диаграмму направленности (каналы могут соответствовать различным частотам
и/или различным угловым смещениям диаграммы направленности на одной частоте,
как в случае двумерного картографирования). Если потребовать, чтобы в разных
каналах "наблюдалось" одно и то же "небо", то функция f(![]() ,
используемая для генерирования источников, должна мажорировать диаграммы
направленности всех каналов одновременно.
,
используемая для генерирования источников, должна мажорировать диаграммы
направленности всех каналов одновременно.
Рассмотренные выше алгоритмы реализованы в применении к радиотелескопу РАТАН-600 на языке C++.
В качестве платформы выбрана операционная система Windows 95. Такой выбор обусловлен возможностью работать с 32-разрядной "плоской" моделью памяти, а также наличием в этой системе мощных средств программирования.
Так как система моделирования работает в пакетном режиме и не требует графического интерфейса пользователя, для неё был выбран режим сборки "Win32+console".
3.2. Структура входных и выходных данных
На входе система имеет иерархическую базу данных наподобие system registry Windows 95. Физически база данных представляет собой набор текстовых файлов, определённого формата.
Каждая строка такого файла имеет вид "идентификатор =тип_данных данные". В конце файла (узла) должна стоять строка "END".
По идентификатору осуществляется доступ к данным; тип_данных — это одиночный символ, стоящий непосредственно за знаком “=”: для целых чисел это “i ”. для действительных — “г”, для строки текста — “s”, для связи с другим узлом —“@”, для ссылки — “>”.
После знака “@” должно стоять имя другого файла базы данных. Система связей должна образовывать дерево.
В одном и том же узле разрешается иметь данные с совпадающими идентификаторами, которые интерпретируются в этом случае как массив и имеют доступ по индексу в порядке следования записей в узле.
Программный интерфейс к базе данных оформлен в виде класса C++ data. Для активизации базы данных достаточно вызвать конструктор этого класса с именем
корневого файла в качестве параметра, например, оператором
data *model = new data("model.df");
После этого доступ к данным осуществляется из корневого узла (который в данном случае отмечен указателем model) компонентными функциями getinteger, getreal, getstring, и getnode, первым параметром которых является строка с идентификатором данных, второй параметр (необязательный) служит индексом, если идентификатор
Например, выражение
model->getnode("CHANNELS")->getnode("CHANNEL",3)->getreal("LAMBDA")
возвращает длину волны третьего канала (при текущей конфигурации базы данных).
Дополнительное удобство такой организации входных данных состоит в том, что для объектов системы моделирования можно предусмотреть узлы, содержащие все данные, необходимые для инициализации (либо ссылки на них). При этом всё, что нужно сделать для создания объекта — это передать указатель на нужный узел соответствующему конструктору.
Например, объект *CMB_spectrum, соответствующий спектру реликтового излучения, создаётся оператором
spectrum *CMB_spectrum = new spectrum( model->getnode("SKY")->getnode("BGROUNDS")->getnode("SP_CMB")
);
Для диагностики возможных ошибок, связанных с неправильной адресацией, в
каждом узле есть запись, обозначающая его тип (узел "SP_CMB" из предыдущего примера имеет тип "SPECTRUM" ). Эта запись проверяется конструктором, и если тип узла не соответствует типу объекта, генерируется ошибка. Предусмотрена также стандартная обработка ошибок в других ситуациях, например при несоответствии типа записи типу функции, использованной для доступа к ней, при обращении к несуществующему идентификатору и т.п.
Аппарат ссылок, предусмотренный в этой базе данных, даёт возможность не создавать копий одной и той же информации, если она нужна в разных местах: там достаточно поместить ссылки. При этом доступ к информации осуществляется по идентификатору ссылки теми же функциями, что и обычно.
База данных содержит информацию о космических сигналах различной природы (узел "SKY"), об аппаратной конфигурации инструмента (узел "CHANNELS") и о задании на моделирование (узлы "SKYJOB", "GEOMETRY").
Данные по параметрам частотных каналов соответствуют текущему состоянию инструмента.
Выходные данные системы моделирования представляются в стандартном для РАТАНа-бОО формате f-файлов и соответствуют откликам каждого вида космического радиоизлучения во всех каналах, а также суммарному многочастотному сигналу (см. Приложение С).
3.3. Структура системы моделирования
Так как космические фоновые излучения делятся на непрерывные и дискретные, то система моделирования обзора должна содержать модули (для C++ —классы ). генерирующие соответствующий выходной сигнал.
Сигнал непрерывного фона в данной системе генерируется объектом класса ехдеп. Конструктор этого класса получает в качестве параметра указатель на узел типа "BJOB" базы данных, который в свою очередь ссылается на конфигурацию инструмента ("CHANNELS"), спектр фона, подлежащего генерированию, а также содержит некоторые другие параметры. Объект класса ехдеп содержит подобъекты классов multibeamf (вычисление преобразований Фурье диаграмм направленности различных каналов РАТАНа-600) и spectrum (вычисление спектра фонового излучения). Для запуска процедуры генерирования используется компонентная функция generate, для записи на диск полученных результатов — компонентная функция flush. Алгоритм генерирования сигнала описан в разделе 1.
Для генерирования сигнала дискретных источников используется
объект класса diogen, конструктор которого работает с узлом типа "DJOB"
базы данных. Этот узел содержит ссылку на конфигурацию радиотелескопа,
данные по зависимости LogN/LogS для текущей популяции радиоисточников (узел
"NS"), основную длину волны, пределы по плотности потока для этой длины
волны и некоторые служебные параметры.
В объект этого класса входят подобъекты классов multibeam(вычисление
диаграмм направленности различных каналов) и sstatistics (генерирование
одиночных радиоисточников). Компонентные функции generate и flush имеют
то же назначение, что и в предыдущем случае. Алгоритм генерирования описан
в разделе 2.
Следующие действия, связанные с обслуживанием объектов классов exgen и diogen, выполняются имеющим диспетчерские функции модулем main:
• Запуск процедур генерирования.
• Запуск процедур записи результатов на диск и уничтожения отработавших объектов.
• Получение и запись на диск суммарного сигнала.
1. Выделение сигнала на фоне космических помех
"Геометрические" особенности радиотелескопа РАТАН-600, имеющие значение при проведении данного эксперимента, таковы:
• Как пассажный инструмент, РАТАН-600 лучше всего приспособлен для наблюдения одномерных сечений неба, поэтому следует исходить из одномерных угловых спектров сигнала; следует также рассмотреть возможность получения углового спектра реликтового излучения из одномерных данных.
• РАТАН-600 обладает значительным избыточным разрешением при наблюдении сахаровских осцилляций: каналу 1см соответствует разрешающая способность 5".l. в то время как для сигнала осцилляций характерны масштабы более 0°.2. Это приводит к тому, что диаграмма направленности мало сказывается на форме спектров сигнала на интересующих нас масштабах.
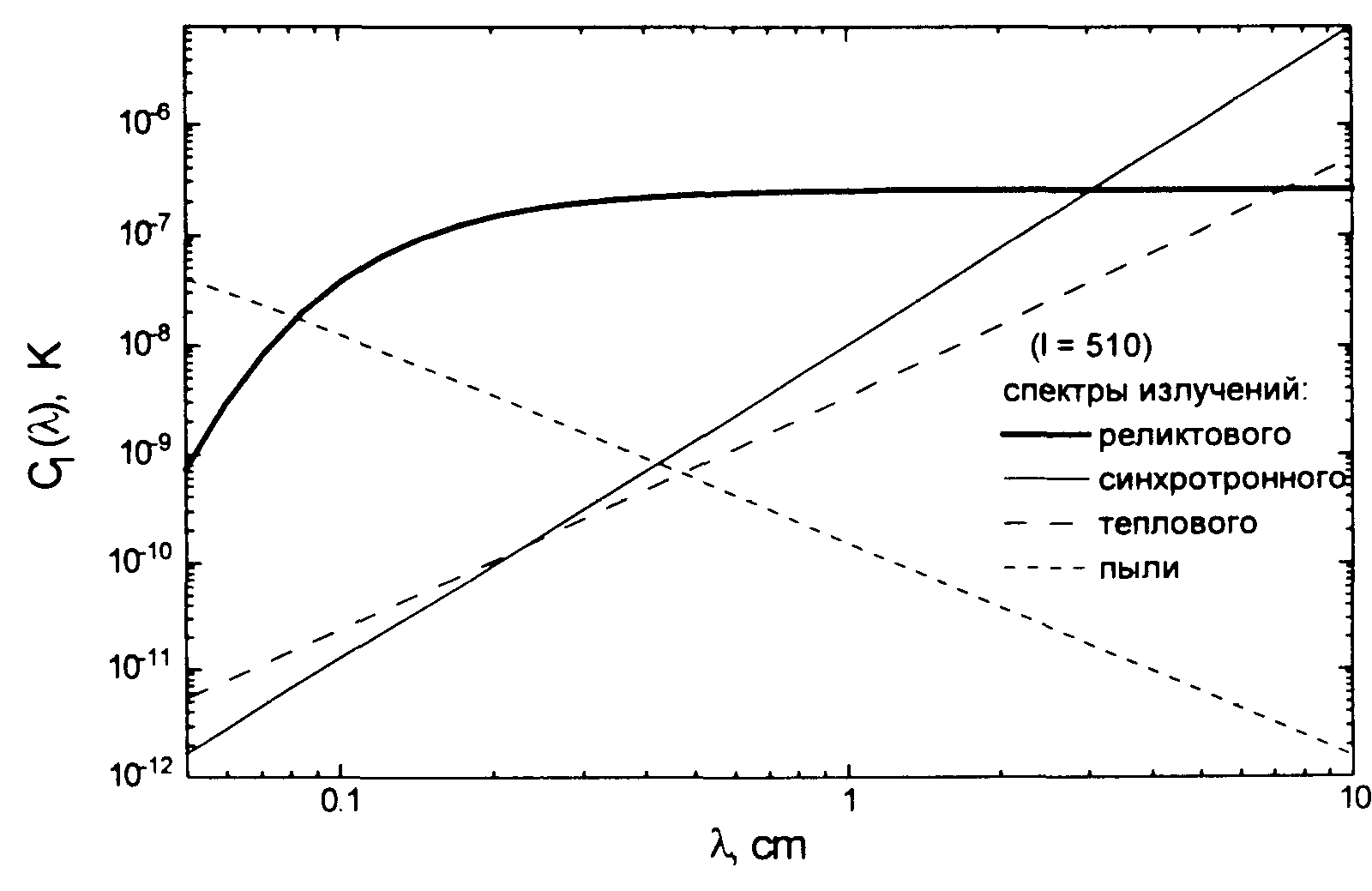
Из Рис. 1 видно, что "галактическое окно прозрачности" (то есть диапазон длин волн, в котором доминируют флуктуации реликтового излучения) простирается от 0.1см до 2-3 см.
С учётом реального диапазона РАТАНа-600 и радиопрозрачности атмосферы, выбор длин волн в этом случае крайне невелик: это либо 1см, в минимуме атмосферного поглощения между кислородным и водяным пиками, либо 2.7см, на длинноволновой границе окна.
Рассмотрим подробнее эти две возможности с учётом специфики инструмента.
Угловые спектры выходного сигнала непрерывных фоновых излучений для каналов 1.0см 2.7см, вычисленные в соответствии с (B.I), (В. 15) и (А.З) показаны на Рис.2 и Рис.3.

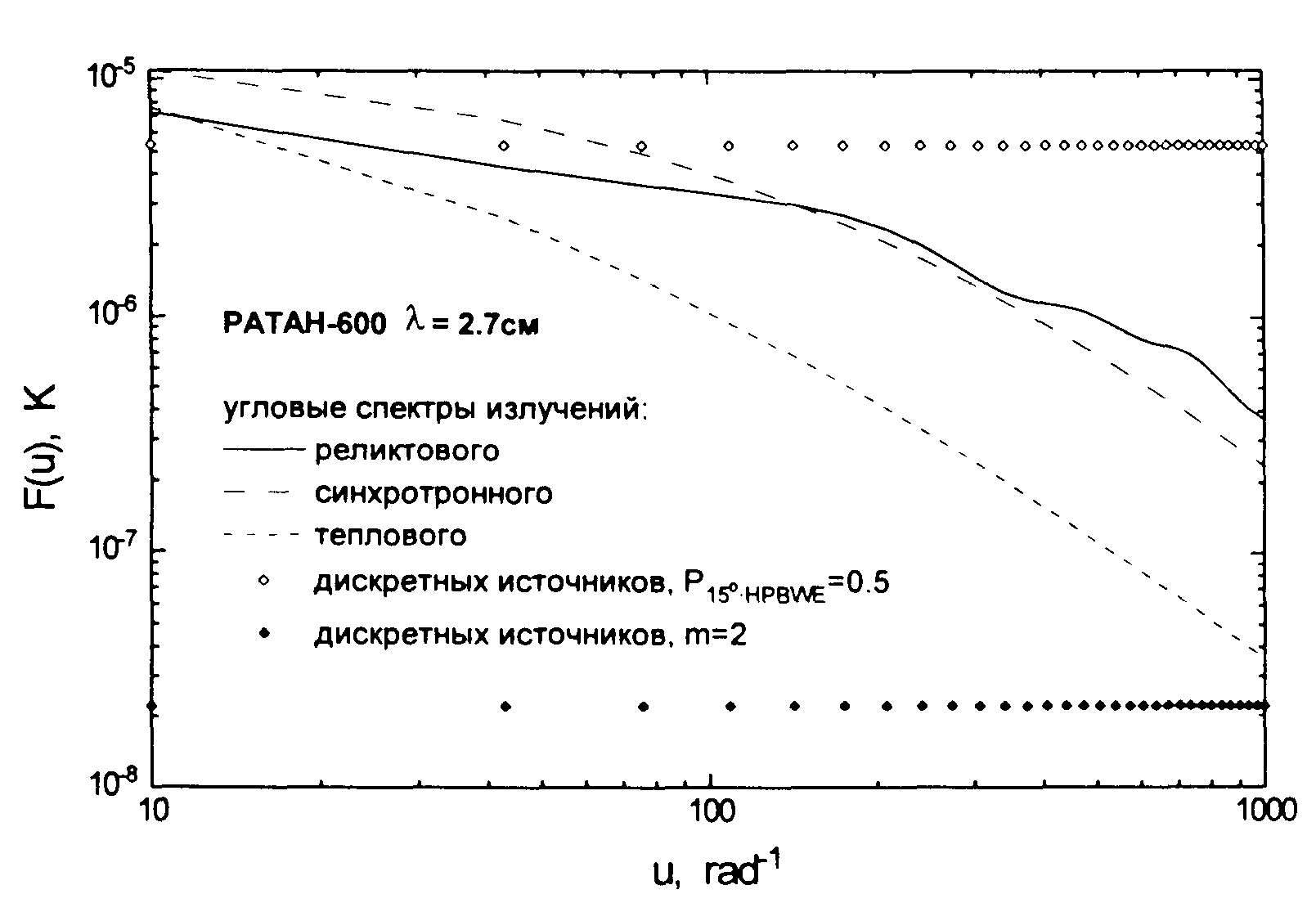
Между этими двумя крайностями, дающими отличающиеся на несколько порядков результаты, находится большое количество паллиативных вариантов, которые могут дать некоторый выигрыш по сравнению с "пассивной стратегией".
Отметим, что нелинейная фильтрация источников в одномерном режиме не даёт никакого преимущества перед устранением избыточного разрешения линейным фильтром типа скользящего среднего (это подтверждается обработкой результатов компьютерного моделирования), поэтому такой режим обработки в рассмотрение не включается.
3
Как видно из Рис. 2, на длине волны 1см сигнал анизотропии реликта доминирует над всеми остальными компонентами. Для дискретных источников проходит даже "пассивный вариант" с селекцией данных; только в районе третьего пика, возможно, следует осуществить какой-то вариант удаления источников.
На длине волны 2.7см (см. Рис. 3) ситуация, как и следовало ожидать, по всем параметрам хуже. Во-первых, следует учитывать сигнал синхротронного излучения, который по данной оценке составляет заметный вклад. Возможно, его придётся вычитать, используя данные более длинноволнового канала, например 7.6см. Кроме того, потребуется отдельная наблюдательная программа для определения параметров дискретных источников, попадающих в полосу обзора, до уровня приблизительно 20mJy (варианту с селекцией данных соответствует граничный поток 2OmJy, см. Табл. 1, а как видно из Рис. 3, требуется улучшение приблизительно на порядок).
При такой картине представляется естественным выбор канала с длиной волны 1см в качестве основного в эксперименте по поиску сахаровских осцилляций (см. также Приложение С Рис. 1, 2 ). Однако следует помнить о влиянии шума атмосферы, который на длине волны 1см, конечно, больше. Поэтому следует сохранить канал 2.7см в качестве резервного на тот случай, если методика подавления атмосферного шума окажется недостаточно эффективной.
Для оценки этого количества были получены модельные записи сигнала анизотропии реликта в канале 1см суммарной длиной 1700° (см. Рис. 4).
По этим данным с учётом (В. 14) было проведено восстановление одномерного спектра мощности выходного сигнала, который, как уже отмечалось, мало отличается от стрип-интеграла исходного двумерного спектра.
' стандартная запись имеет длину 1h на небольшом склонении это составляет 15°, что учтено при определении площади ? .
4
Примеры результатов моделирования

Рис. 1. РАТАН-600, канал 1.0 см, длина записей 15°. Сверху вниз: суммарный сигнал, реликтовое излучение, синхротронное излучение, тепловое излучение, излучение пыли, дискретные источники с крутым спектром, дискретные источники с плоским спектром.

Рис. 2. РАТАН-600, канал 2.7 см, длина записей 15°. Сверху вниз: суммарный сигнал, реликтовое излучение, синхротронное излучение, тепловое излучение, излучение пыли. дискретные источники с крутым спектром, дискретные источники с плоским спектром.
2
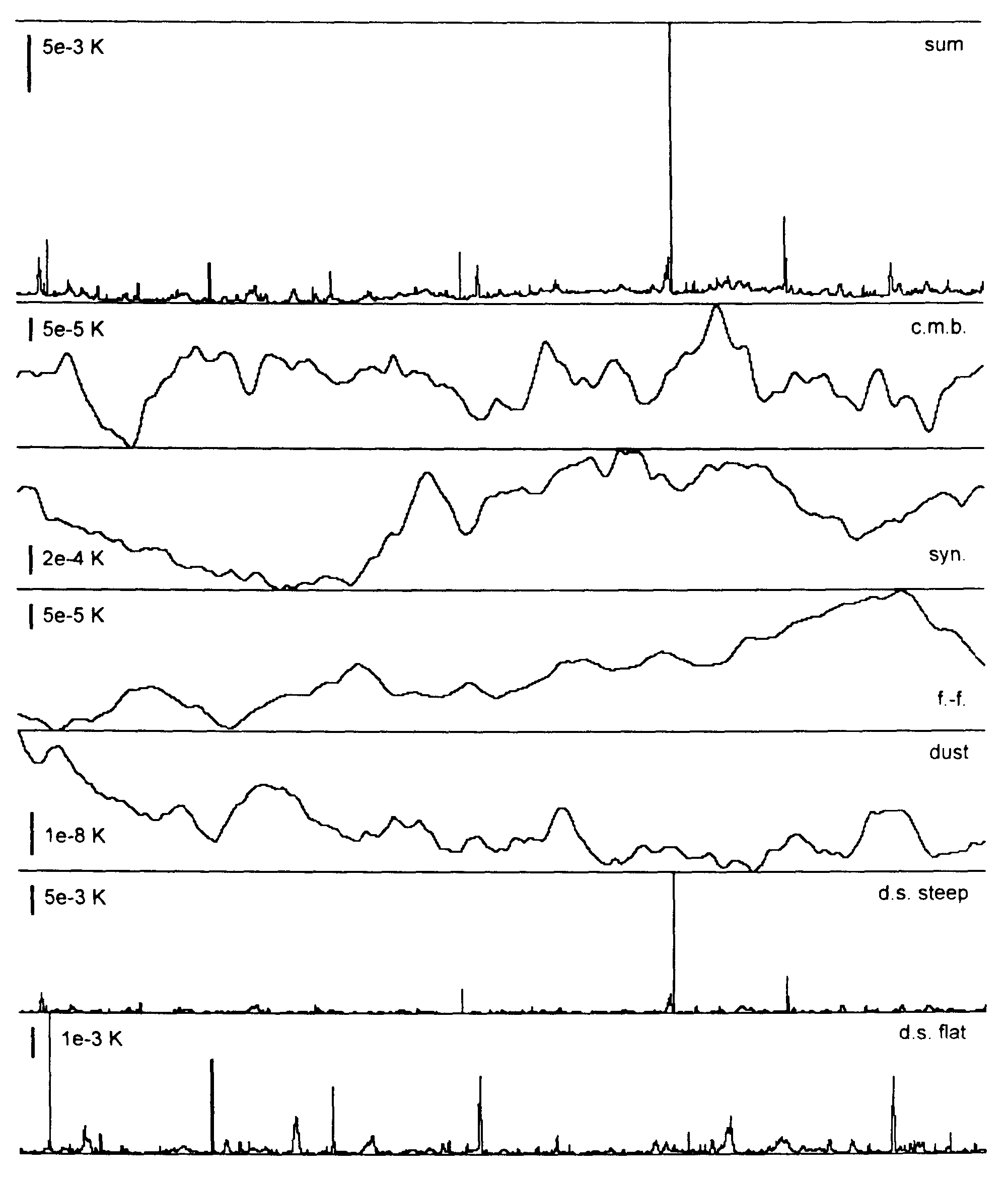
Рис. 3. РАТАН-600, канал 3.9 см, длина записей 15°. Сверху вниз: суммарный сигнал, реликтовое излучение, синхротронное излучение, тепловое излучение, излучение пыли, дискретные источники с крутым спектром, дискретные источники с плоским спектром.

Рис. 4. РАТАН-600, канал 7.6 см, длина записей 15°. Сверху вниз: суммарный сигнал. реликтовое излучение, синхротронное излучение, тепловое излучение, излучение пыли, дискретные источники с крутым спектром, дискретные источники с плоским спектром.

Рис. 6. РАТАН-600, канал 31.0 см. длина записей 15° . Сверху вниз: суммарный сигнал, реликтовое излучение, синхротронное излучение, тепловое излучение, излучение пыли. дискретные источники с крутым спектром, дискретные источники с плоским спектром.
Литература
Литература
1. Franceschini A. Et al, The Astrophysical Journal, 344,
35, 1989.
9