Experiment COLD
main page
previous chapter
next chapter
 JSEC Astronomy 
main page
 

4. Limiting Factors and Characteristics of the RATAN  
 

4.1. Theoretical Sensitivity of the Radio Telescope and the Problem of Attaining it in Practice

The 7.6-cm radiometer described above definitely has very good characteristics; the amplifier itself has a noise temperature of approximately 10 K and a bandwidth of 500 MHz. Therefore, the problem of actually obtaining these characteristics in practice was particularly acute. The problem was divided into the "internal" (or engineering) problem of achieving the highest possible sensitivity (lowest possible noise); the problem of actually obtaining this sensitivity from the radio telescope-radiometer system with short integration times; and, finally, the problem of obtaining the maximum possible sensitivity in the essentially unknown field of studying extended regions of the sky at surface brightness levels of 1 mK or flux densities of 1 m Jy.*

In Experiment Cold, we dealt with all of these problems. We shall now list the limiting factors:

*1 mJy = 1 millijansky = 10-29 watts m-2 Hz-1, and 1mK = 10-3 K.
  The first three items above are internal factors; they determine the average system noise temperature and its stability. The remaining items are, in essence, various types of external additive interference* which are impossible for us to eliminate; we can merely attempt to reduce their influence by applying various filtering or cleaning methods. The higher the sensitivity of the radiometer, the more perceptible the influence of these factors is, and each of them eventually becomes a problem in itself. As was shown in the previous section, we were able to obtain very good performance with respect to the first three items, and actually obtain the theoretical receiver sensitivity in practice through the efforts of the engineers. Before we go on to discuss the known properties of some of the external factors and the possibilities for dealing with them at the RATAN, we shall remind the reader how sensitive modern radio telescopes can be in theory (the sensitivity can be determined from the average noise level in the radio telescope – radiometer system). It is customary to characterize the internal noise by an effective noise temperature at the input of the receiver system. If the system noise temperature is Tn, the minimum measurable increase in the antenna noise temperature Ta. caused by a useful noise signal (when pointing the antenna at a source) is (Esepkina, et al., 1973):

*Multiplicative interference, such as modulation of the emission from a source by random variations in the atmospheric absorption coefficient, for example, are not significant for the problems we are studying.
 

 

(4.1)
 
where Df is the input bandwidth, DF = 1/4t is the bandwidth of the output filter (or t is the integration time), and a1 is a coefficient which depends on the radiometer design. In modern centimeter-wavelength receivers, noise temperatures of 10 – 20 K (and even lower) are achieved by using masers, cooled parametric amplifiers (ps in our case), and, very recently, cooled transistor amplifiers with field effect transistors (FETs). As we saw in the preceding section, the sky noise (the average noise temperature of the atmosphere and cosmic background radiation) and the noise from the ground are added to the receiver noise temperature, and the total noise temperature of the radio telescope turns out to be approximately 40 K for large instruments; for small, specialized instruments, Tn  may be somewhat lower. At these low noise temperatures, the sensitivity in terms of antenna temperature is approximately 10-3 K for an integration time t =1 s and D f = 1 GHz, according to Eqn (4.1). The sensitivity in terms of the flux density from a point source is
 

for an effective collecting area of 1000 m2. A further reduction in DTa and DPmin is possible, in principle, if the integration time is increased. These are the kinds of numbers we should aim for.

However, the actual state of affairs is not determined by Eqn (4.1) but by the sum

(4.2)
where the Ti are the root-mean-square fluctuations in the interference caused by the factors listed above. Because of the non-Gaussian nature of this interference, the actual fluctuations at the output of the radio telescope, DTS, may exceed the theoretical temperature fluctuations DTa by a factor of a few hundred; only for the latter does Eqn (4.1) hold, and a relationship between DTa  and Tn  exist (via the radiometric gain . The noise from any one of these interference factors cannot, as a rule, be characterized by a single parameter; this type of noise requires many parameters to describe it, and has a complicated (and unstable!) correlation function (the correlation function for the white noise in the radiometer is, by nature, a d-function). Both experiment and the modern theory of the observation of signals against a background of noise suggest that the classical approach is to find the solution to the optimal filtering problem, where the frequency response curve of the receiver system is the complex conjugate of the signal spectrum. Such filtering can be obtained in practice if a priori information about the spatial frequency spectrum of the object being studied* and information about the spectra of the noise sources listed above are used. Unfortunately, the observer frequently has neither one nor the other. Later, we shall see that we in fact have a way out, in which the procedure of constructing an optimal filter acquires a unique sense: we artificially transform the noise and signal spectra to an "optimum" form, sacrificing a portion of the signal spectrum in the process (e.g., in a region with anomalously high noise), i.e., we a priori consent to a loss of some of the information, but retain some hope of obtaining information on certain components of the spatial spectrum of the signal, or on corresponding scales on the sky. We shall now discuss the sources of interference and the methods known for overcoming the interference associated with these sources, as well as the characteristics (advantages) of the RATAN which could be utilized in carrying out Experiment Cold so as to be reasonably confident of its success.

4.2.3 Atmosphere

The clearest example of the type of interference discussed above is the emission from the atmosphere. With an average atmospheric emission temperature of approximately 2.5 K at 7.6 cm (about 10% of the total system temperature), the dispersion in the atmospheric interference (defined as the root-mean-square deviation from the average over a time interval of 1 hr) in all of the Cold experiments was a factor of 100 greater than the theoretical radiometer sensitivity (averaged over two months of observations). As is well known (Esepkina et al., 1973; Kaidanovskii et al., 1982), when observing sources of small angular diameter (on the order of a few beamwidths in size), an effective filtering method is widely used – double-beam observations (in which the antenna records the difference in the emission from two adjacent directions – source and background). In our case, the observations were, by necessity, carried out using a single beam and, because of this, other filtering methods were necessary. Two methods seemed promising:


*Due to the motion of the source through the antenna pattern, the spatial frequency spectrum is transformed into a time spectrum at the receiver output, which is then analyzed.
 
 

suppressing the low-frequency fluctuations during the data reduction, and using the correlation between the atmospheric emission at various wavelengths for cleaning. Let us briefly explain these two methods. At Pulkov and the RATAN, a fair amount of experience has been accumulated in studying the fluctuations in the atmospheric emission and suppressing them; this experience has been reviewed by Kaidanovskii et al. (1982). Two important conclusions follow from the measurements of the fluctuations in the emission from a cloudy atmosphere* that have been carried out at the RATAN over the last few years:

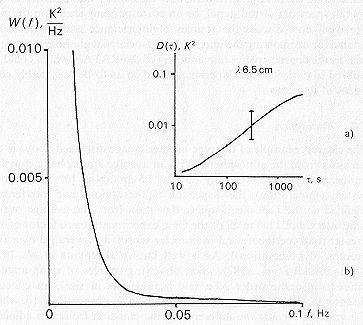
Figure 4.1 (a) An example of the structure function observed at the RATAN-600 for the fluctuations in the radio emission from a cloudy atmosphere. (b) The spectrum of the fluctuations in the atmospheric radio emission corresponding to structure function (a).


*Fluctuations in clear weather have not been sufficiently studied, since they are at a much smaller level and only become apparent when the observations are extremely sensitive.

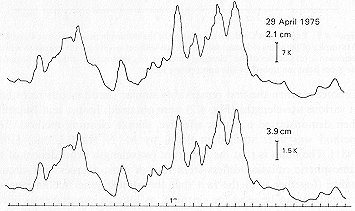
Figure 4.2 The radio emission from clouds at 2.1 and 3.9 cm (from observations at the RATAN-600 with the antenna stationary). The correlation of the emission at these two wavelengths is very striking; the intensity of the emission is proportional to l -24
 

Figure 4.3 Experiment Cold: (a) correlation of the atmospheric emission at 4 and 8 cm; (A) samples of the scans (65 scans were averaged without selecting with respect to weather conditions); (c) samples of the "cleaning" process, i.e., subtraction of the 4-cm Scan from the 8-cm Scan multiplied by the appropriate factor.

 Timofeeva when the first remarkably similar simultaneous recordings at various wavelengths (Fig. 4.2) were obtained; Ipatov and Bulaenko then demonstrated a rather effective, simple cleaning method. This method was later studied in detail by M. N. Kaidanovskii (1980, 1981). The point is that the spectrum (wavelength dependence) of the atmospheric emission differs from that of most sources; this circumstance (together with the fact that the atmospheric fluctuations are correlated) can be used for cleaning, as long as simultaneous observations are made at several different frequencies. In the cycle of Experiment Cold discussed here, observations were made at wavelengths of 1.35, 2, 3.9, 7.6 (the main wavelength), 8.2, and 31 cm. The observations at the shorter wavelengths (2 and 3.9cm; see Fig. 4.3) were used to remove the effects of the atmosphere from the images at 7.6 cm. When testing the correlation method (Kaidanovskii, 1981), we succeeded in suppressing the fluctuations in the atmospheric emission by approximately a factor of 10 (or somewhat more).*

Vitkovskii has proposed an interesting, simple method of dealing with strong atmospheric interference:

Suppose we have several scans of the same piece of sky which are of various quality (more precisely, with different contributions from atmospheric noise). The best of these scans (assume that it is the first) is then adopted as a reference for which the contribution from atmospheric noise can be neglected to first approximation. Then, all of the remaining records can be made so that they are no worse than the reference scan. In fact, subtracting the first record from the second, we remove the emission from sources, the Galaxy, and the Universe, and the remainder gives.us the contribution of the atmosphere to the second scan (since the contribution to the first is assumed to be zero), and so forth. These atmospheric components can be subtracted from all the records. This method was tested on 22 scans of the section 13h < a < 14h of Cold-1. This is successful provided

 
where smin and smax are the minimum and maximum dispersions in the atmospheric noise in the observations on the various days, and N is the number of observing days. It is clear that the averaged scan contains all of the atmospheric noise in the best scan (independent of N). However, the atmospheric conditions are so variable that inequality (4.3) is almost always satisfied, and such cleaning makes sense.

 
4.3. Confusion Noise

The noise-like fluctuations which arise as the antenna pattern moves over a sky filled with faint background sources is called "confusion noise". If the distribution of such sources over the sky is random, the


*It should be noted that sufficient experience in cleaning by correlation has not yet been accumulated. From the available experience, it seems that the "worse" the atmosphere, the better it is cleaned; as for a "good" atmosphere (for example, clear weather), the amount of experience is obviously insufficient.
 
 

power at the output of the radio telescope will also vary in a random fashion. These fluctuations are not removed by long integration times, and they are diferent for diferent radio telescopes. If the "number of sources – flux density" curve (logN–logP, see Fig. 6.5) is known accurately, it is possible to estimate the confusion noise. In order to do this, however, it is necessary to know the shape as well as the eftecive solid angle of the antenna pattern of the radio telescope. This is essential when comparing the RATAN-600 to paraboloids. For the RATAN, the confusion noise becomes progressively smaller (according to the variation in the excess resolution coefficient h (see Section 4.6 for a discussion of the coefficient h)) as each of the following observing modes is used:

It will be recalled that the wavelength dependence (confusion noise ~l-2.75) can also be used to reduce confusion noise. On the other hand, in large aperture synthesis systems (with a large value of h, and, therefore, high sidelobe levels), it is necessary to take the role of faint background sources which fall within the sidelobes into account; as a rule, they play the decisive role in very large VLA-type arrays. On the linear portion of the log N – log P curve, the observers at Areceibo recommend the following simple formula for estimating the "confusion noise":
DP = 3700 (n[GHz]) -0.7  ž ( W [sterad]) Jy.

In more complex cases, Scheuer suggests the following relationship:

 
DP  P1

where P1 is the flux density at which the surface density of sources is one radio source per antenna beam. However, if we are interested in sufficiently large regions of the sky, it is possible for high-resolution instruments to overcome confusion noise. We shall discuss this in more detail in the following section.
 

4.4. Elimination of Discrete Sources

Usually, "specialization" of radio telescopes calls for a certain division of labor: aperture synthesis instruments study the discrete sources, while small antennas (including horns and dipoles) study the background emission. However, if the requirements on the accuracy with which the background emissioon is measured are increased, the background from faint (and bright!) radio sources inevitably becomes a limitation for low-resolution telescopes. If the contributions from such radio sources are not taken into account when observing, then, using the log N – log P curve (for a given wavelength), it is possible to find the limitations on the accuracy with which the surface brightness of extended features can be measured. The calculations carried out by Daneze et al. (1982) using the latest log N – log P data are shown in Fig. 4.4. The RATAN-600 allows the contributions from interfering sources to be taken into account to first order, down to a level of at least a few millijanskys (in Experiment Cold), i.e., the beam size of the radio telescope is much smaller than the region of background emission being studied. Essentially, the confusion noise can be reduced by at least a factor of 10 on scales of ~10'. See Fig. 6.4 for an illustration of the procedure by which sources were removed using Gaussian analysis. The next step in taking sources into account more carefully consists of complex studies of the same region using aperture synthesis instruments (the discrete sources) and the RATAN-600 (the background with the sources subtracted out); at present, the inability of aperture synthesis instruments to study large regions of the sky is the limitation here. Discussions are currently under way to organize observations of this type in a collaboration between the RATAN and the VLA.

Figure 4.4 A theoretical estimate of the limitations imposed by confusion noise on the ability to measure fluctuations in the three-degree background. The levels reached in the present work (by taking resolved radio sources into account) on scales of 10' and 1o.5 are indicated by the arrows below the curve.
 

4.5 Sky Surveys Using the RATAN-600

Carrying out surveys of the sky is one of the fundamental branches of astronomy. Without such surveys, our picture of the Universe is incomplete. The catalogs compiled when carrying out a sky survey are the basis for detailed studies by any of the methods available to humanity. The ideal survey would cover the entire sky at the highest sensitivity (and resolution!) available with current radio telescopes. But, since radio astronomers have not been able to develop a radio telescope for an experiment of this type, it is necessary to restrict ourselves to "specialized" surveys: to carry out either a rapid (rough) survey of the entire sky (paraboloids), or extremely deep surveys of very small sections of the sky (VLA). It is clear that the higher the desired sensitivity of the survey, the more difficult it is to survey a large section of the sky. Therefore, the extremely deep VLA surveys have little statistical significance (Keller-man, 1982), and the so-called rapid, "complete" surveys with para-boloids contain only the very strong sources, of which there are, once again, very few (see Kellerman, 1974).

The RATAN-600 occupies an intermediate position with respect to surveys. It is the only radio telescope at which a study of the entire sky with a resolution of 15" – 1' at wavelengths of 2, 3.5, and 8 cm, and a sensitivity higher than that of the so-called "strong-source surveys" is currently being carried out.

At its most sensitive wavelength, the VLA can make a map of a 1' x 1' region of the sky with an RMS noise level of approximately 0.08 mJy in 8 hr of synthesis. True, 8-hr exposures are also possible at the RATAN, but at present, only in the region near the North Pole. Here, in this limited region, the same flux sensitivity as the VLA can be obtained. However, the struggle for statistically significant material leads to another mode of operation, where a significantly larger section of the sky can be studied in the same amount of observing time (at the price of a loss in sensitivity), and a larger number of sources are detected. That is, one should pay more attention to the relationship between the region surveyed, the sensitivity and the number of sources. The high sensitivity of the VLA (0.08mJy) is achieved through a prolonged synthesis of a very small region. Transforming this to t = 1 s, this corresponds to an RMS of about 1 may; the RATAN-600 has a comparable sensitivity for  t=1s (~ 5mJy), but even when observing with only one sector, the emission (integrated) from a 1' x 10' region (for observations using the plane periscopic refector on the south sector, a 1' x 40' region) is recorded. Because of this, a region which is a factor of 105 larger than at the VLA is surveyed in the course of 8 hrs of observations. It is possible to develop a way of carrying out such a survey in which the number of sources observed is as large as possible. Observations near the equator using the periscopic reflector of the RATAN (with a broad field of view in the vertical direction – approximately 40') turned out to be almost ideal from this point of view. In this mode, the RATAN-600, together with the high-sensitivity radiometer described in the previous section, has a record-breaking productivity – several hundred radio sources per day, which is approximately equal to the total number of radio sources which have been observed to date in all centimeter-wavelength surveys.

Thus, we see that there are two methods of increasing the number of sources: increasing the depth to which a small fixed region of the sky is surveyed (increasing the exposure), and actually increasing the area surveyed. It is easy to show that where the log N – log P curve is steep, the former is more efficient, while for extremely faint surveys, where the slope of the log N – log P curve is small, the latter is considerably more efficient. This method is widely used at the RATAN-600, and this method was chosen as the basic method for Experiment Cold in particular.
 

4.6. Brightness Temperature Sensitivity

If a radio telescope is attached to a matched load, the source and telescope are in thermodynamic equilibrium: all of the power received by the radio telescope from a distant object of arbitrary shape is reradiated back into space by the radio telescope. If we received radiation from the cosmos from an isotropic background with a temperature of 2.7 K over an angle of 4p sr, the so-called "effective antenna temperature" of the load resistance would be exactly equal to the brightness temperature of the background, i.e., 2.7 K. When studying an object of finite extent, it is necessary to know the shape of the source as well as the complete antenna pattern, i.e. the intensity of the radiation emitted by the radio telescope in all directions (over 4p sr). Only in this case is it possible to calculate the coefficient for the transformation between brightness temperature and antenna temperature. This calculation is based on thermodynamic arguments, since it is necessary to find out how much of the radiation emitted by the radio telescope will not be emitted toward the source of the radio emission. We shall take these losses into account using the two coefficients h1, and h2 , where h1, involves the losses in the antenna system (spillover and scattering from errors in the surface), and h2, takes the ratio of the solid angles (and the shapes) of the source and antenna pattern into account. Thus, we write the relationship between the brightness temperatures and antenna temperature as

The RATAN-600 is one of the rare instruments for which the antenna pattern has been studied over nearly an angle of 4p (see Section 2.4). If the size of the object being studied, W0, is less than (l/l)2 (where l is the correlation radius for the surface errors), but larger than the main beam of the antenna WA, the coefficient h1, in the relationship between TA and TB can be written as

where

It is assumed that W0 << (l/lm)2 and Wm << (l/lm)2 .  The measurements of Korol'kov and Maiorova (1978), and the research done on the antenna pattern done by Soboleva, Krat et al. (see Golosova et al., 1982) make it possible to compile the following table:
 
losses due to secondary mirror spillover: 
losses due to main mirror spillover: 
losses due to the gaps between the panels: 
losses due to extended scattering 
(for an RMS surface error of 0.5 mm):		 0.97 
0.80 
0.965 

0.994
 
Altogether, for a source larger than the beam of a single element, h1 = 0.744.

It will be remembered that the aperture efficiency should not be confused with the coefficient h1, (as was done by Partridge (1980)). Moreover, if the errors in the surface are small, in order to make the beam efficiency approach unity, it is a good idea to decrease the aperture efficiency by decreasing the so-called aperture coefficient, i.e., underilluminating the main mirror. In fact this procedure was carried out in Experiment Cold by "refocusing" the system so that the secondary mirror illuminated a smaller portion of the main mirror than in the normal operating mode. As we have already mentioned, in Experiment Cold, the primary feedhorn was moved away from the focus in such a way that the secondary mirror formed a converging wave with the focus at the main mirror, rather than a plane wave. This led to a small RMS phase error over the aperture, but reduced the losses due to spillover (and decreased the antenna noise).

We shall now attempt to take the relative sizes of the telescope beam and the scales on which we are studying the variations in the 3-degree background into account, i.e., determine the coefficient h2,. For scales comparable to the size of the horizon at the hydrogen recombination epoch (several degrees), there is no correction: the entire antenna pattern (as well as the error pattern), which lies within the envelope of the pattern of a single element, is contained in a single inhomogeneity, and only the losses which were discussed above need to be taken into account. The situation is completely different when the antenna pattern is comparable to the size of the inhomogeneities being studied. This case is illustrated for a single inhomogeneity in Figs. 4.5(a – c). The relationship between the antenna temperature and the brightness temperature for each of these three cases is given by

Figure 4.5 The relationship between the antenna temperature and brightness temperature for various ratios of the source size and beam size.

where WA is the effective solid angle of the antenna pattern within the pattern of a single element of the antenna. Here, we neglect all of the coefficients discussed above, but the values of h2, are

 h1=1,             h2=fiy/fAy          and          h2=Wi/WA

respectively. These relations are obvious from the same thermodynamic considerations discussed above. Two points still need to be clarified:

First, the quantity fAy ,. is not the vertical half-power beamwidth of the actual pattern. The antenna pattern of the RATAN-600 is a function of the elevation at which one is observing. For observations on the horizon, the "aperture" (i.e., as in the shape of the main reflecting surface of the RATAN-600 as it appears to an observer looking from the source) is a rectangle, and both cross-sections through the antenna beam (in azimuth as well as elevation) are Gaussian in form. For observations at intermediate elevations (our case), the aperture is shaped like a curved slit. In this case, the size of the center of the antenna pattern remains almost unchanged in azimuth but becomes much narrower in elevation (see Figs. 4.5 and 3.8). If the width of the antenna pattern is approximately fAy = 40' when observing on the horizon, then at the altitude of SS433 (at culmination), the size of the center of the beam in elevation is approximately 10'. However the narrowing of the antenna pattern in elevation occurs through the redistribution of energy over concentric surrounding regions centered on the axis of the antenna pattern. This means that for a roughly circular source, the situation is independent of altitude above the horizon from the viewpoint of thermodynamics. Therefore, without resorting to taking the shape of the antenna pattern into account exactly, we can use the transformation from brightness temperature to antenna temperature for the simple case of a "knife-edge" antenna pattern (i.e., the case of observations on the horizon). Thus, the full width of the antenna pattern at half-power for observations on the horizon (i.e., the size of the antenna pattern of a single element) should be used for fAy  in case (b) above.Second, we are studying the statistical anisotropy of the sky, rather than an isolated fluctuation. We should take the fact that the number of inhomogeneities which simultaneously fall within the antenna beam is diferent for cases (a) and (b) into account. It is easy to see that this number n is equal to 1, fiy/fAy  and Wi/WA respectively. As Bracewell and Conklin showed, taking the number of fluctuations per antenna beam into account leads to the following relationships between theantenna temperature and brightness temperature for cases (a), (b), and (c), respectively:

 

Thus, we must use the following relationships when reducing our data:

In conclusion, we shall make a remark about the relationship between TA and TB for aperture-synthesis antennas. In this case (see Esepkina et al. (1973), and Christiansen and Hogbohm (1972), for example), the coefficient which characterizes the excess resolution or overfilling of the aperture is given by the relation
              (4.8)

where D2 synth is the synthesized aperture, and Wsynth is the solid angle of the synthesized beam, and Seff is the effective collecting area. In large synthesis systems, the coefficient h2 very small, on the order 10-6 for the VLA and 10-10 for VLBI; therefore, these systems have very low brightness temperature sensitivity. For the RATAN, the coefficient h2 , can also be used to characterize the excess resolution obtained in elevation because of the fact that the aperture appears to be curved when observing sources at elevations other than zero (the horizon), as was mentioned above; the value of h2 , can be determined using Eqn (4.8) and Fig. 3.5;

h2 =fAy,synth / fAy0.25
 
From what has been said, we can conclude that an ordinary paraboloid would be the best instrument for studying the background radiation if there were no noise from background sources (confusion noise). The RATAN is less affected by confusion noise (see Sections 4.3 and 4.4); at the same time, it has a rather good coupling coefficient between TB and TA, which allows complex projects (tike the Cold program) in which high sensitivity is obtained in terms of the brightness temperature of extended objects as well as flux density.
 

4.7. Conclusion: The Role of the RA TAN in Modern Radio Astronomy

  As became clear in the 1970's, radio astronomers were incapable of building a completely universal instrument whose capabilities exceeded those of any other specialized radio telescope intended for solving a particular astrophysical problem. This can not be overcome by increasing the amount of money spent – both existing radio telescopes costing 100 million dollars and all of the enormous proposed telescopes costing tens of billions of dollars (such as, for example, the Cyclops project) suffer from this limitation.

Modern radio telescopes have become specialized not only with respect to wavelength region or field of radio astronomy, but even with respect to a model of a typical radio galaxy (see Fig. 4.6). The giant "global" radio telescope networks only see the nuclear sources, which have sizes of ~ 10-3 arsec and a surface brightness very close to the limit, ~ 1012 K. They do not detect any of the main body of a radio galaxy (or, perhaps, they may see nothing at all, if the nucleus of the galaxy is not in an active phase. Moreover, they do not see any other objects – nebulae, H II regions, supernova remnants, main-sequence stars, the Sun, Moon, the planets and their statellites, etc.

The very large VLA-type aperture synthesis instruments only see the integrated emission from the nuclear source and the narrow streams and jets coming out of it, as well as the so-called "hot spots" in the radio components. The extended regions which emit most of the energy are only partially detected, and are sometimes completely invisible. Even the brightest source in the sky, Cas A, all of 4' in size, is completely invisible at the highest resolution of the VLA.

The RATAN-600 can detect the point source in a galaxy nucleus (but only from its integrated emission!) and obtain coarse images of the main body of a radio galaxy, but images of the nuclear source, jets, and hot spots are beyond its reach.

Figure 4.6 The structure of a typical radio galaxy and the capabilities of radio telescopes. Very-long-baseline interferometry is only able to study the nuclear sources with a brightness of 108- 1012 K; the rest is not detected. The largest array in the U.S.A. (the VLA) can not resolve the nucleus, but is able to record the jets and streams near the nucleus and the bright portions of the "hot spots" beautifully. The best aperture synthesis telescope in Europe (the WSRT, Westerbork, Holland) is not able to resolve the nucleus or the jets near the nucleus, but is capable of constructing a qualitative radio image of the components. The RATAN-600 is capable of distinguishing the emission from the nucleus and "hot spots" from the emission of the galaxy as a whole, and, in addition, it is capable of observing low-contrast features (which are not visible by other means) in radio galaxies. Fully steerable reflectors, as a rule, only see the integrated emission and are the ideal means for studying the integrated properties of radio galaxies.

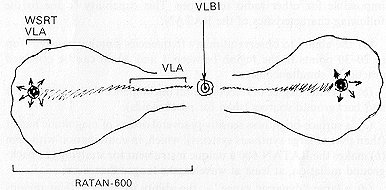
The largest paraboloids in the world are, as a rule, completely incapable of studying the structure of a typical radio galaxy, but they measure the integrated characteristics of radio galaxies very well, and are indispensible for studying the Galaxy, etc. It should be remembered that the bulk of the information on radio source statistics has been obtained using paraboloids at centimeter wavelengths. The fatal characteristic of a completely universal radio telescope is the same as for a person: a generalist knows a little bit about everything, in contrast to a narrow specialist, who knows everything within a very small field. In modern radio astronomy, as in modern society, the era of the Humboldts and Lomonosovs has come to an end. Progress in radio astronomy now occurs through the results obtained using specialized instruments.

In many respects, the RATAN-600 occupies an intermediate position between the large aperture-synthesis systems and the ordinary para-boloids. However, experience has shown that it is difterent from all other radio telescopes in some combinations of parameters; this allows us to use the RATAN-600 for problems which are practically impossible for other radio telescopes. This capability is due to the following characteristics of the RATAN: 

(1) A twenty-four-hour synthesis of an area 1' x 1' in size, and
(2) a survey of the entire strip of sky which passes through the field of view of the radio telescope in a 24-hr period of time.

In the first case, data is collected from a 1' x 1' (10-5 sr) region in 24 hr, but at high sensitivity. In the second case, the 24-hr field of view is 2p rad x 1'  2 x 10-3 sr, with a sensitivity similar to that of the RATAN-600 in sky-survey mode. However, in this mode, the RATAN-600 observes a region 2p radian x 40' = 0.8 x 10-1sr in a 24-hr period, i.e., forty times larger. Therefore, specialization of instruments makes sense: it is efficient to carry out statistical work (but not on objects which are too faint) at the RATAN-600 and extremely deep studies of selected regions using the VLA.

 In the next section, we shall describe how we selected the problems best suited to the capabilities of an almost ideal radiometer. 


August 24 1998,  stokh@brown.nord.nw.ru